Nowa wizja (praw) Przyrody
Krzysztof Zawisza (ur. 1963 w Lublinie). Fizyk teoretyk, filozof, prozaik, poeta. W latach 90-tych laureat ogólnopolskich konkursów literackich w kategoriach poezji i prozy. Obecnie związany z Katolickim Uniwersytetem Lubelskim. Autor oczekujących na publikację prac naukowych w dziedzinach filozofii, logiki, matematyki, fizyki i astronomii. Najważniejsze z nich to:
1.
Pełny system dedukcyjny. Podstawy oraz niektóre z zastosowań
[tekst dotyczący możliwości dokonania pełnej arytmetyzacji języka naturalnego,
przewidywanej przez R. Lullusa i G.W. Leibniza].
2. Nowe spojrzenie na problem antynomii w logice
[przedyskutowana praca, zawierająca propozycję rozwiązania problemu
antynomii logicznych, m.in. słynnego paradoksu kłamcy];
3. Czerwona
nić w dziejach kosmologii, czyli Filolaos z Krotonu [zrecenzowana
praca; ukazała się w kwietniu 2006 w Internecie na stronach pisma „Gnosis”
i oczekuje na wydanie książkowe w Wydawnictwie AKME w Warszawie];
4. Wielkoskalowa Struktura Wszechświata. Konieczność
vs. przypadek [wielokrotnie pozytywnie naukowo zrecenzowana praca,
dotycząca odkrycia ‘Reguły Przypadku’; na jej podstawie powstał artykuł
pt. A NewProbabilistic Measure as the Explanation of a Geometrical
Order in Nature];
5. 4-D Horn Hypertorus as the Model of Spacetime
[propozycja rozwiązania problemu przyspieszania ekspansji Wszechświata
oraz łamania symetrii CP].
6. A New Natural Arithmetic with Division by zero
and its Physical Consequences [Propozycja rozwiązania liczącego 1200
lat problemu dzielenia przez zero i przy jego pomocy wprowadzenia Ogólnej
Teorii Pola w fizyce] .
Prywatne zainteresowania i hobbies: psychologia, literatura, religioznawstwo, tenis, badminton, broń wiatrowa.

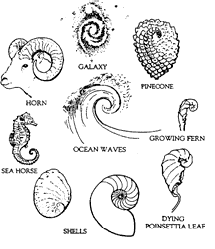
w różnych zjawiskach i obiektach






[...]
przyroda jest pełna wzorów. [...] Obcowanie z przyrodą jest dobre dla
nas wszystkich: przypomina nam kim jesteśmy.
[...] matematyka jest nauką o wzorach, a przyroda wykorzystuje każdy istniejący
wzór.
Każdy z wzorów przyrody jest zagadką, prawie zawsze głęboką.
Może zrozumiemy pewnego dnia, dlaczego przyroda wybiera te symetryczne
formy.
I. Stewart, Liczby natury,
tłum. M. Tempczyk,
Warszawa 1996

www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/
Poniżej natomiast zaprezentujemy przykłady w większości nowe.
Dan Brown, Kod Leonarda da Vinci,
tłum. Krzysztof Mazurek, W-wa 2004, s. 123.

a-b - Pierścienie Saturna
c - Rdzeń geologiczny
d - Rozkład linii widmowych w czerwonej części światła słonecznego
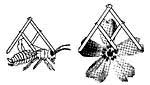
Pszczoła, kwiatostan

Układ Słoneczny
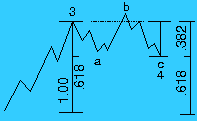
Wykres wahań kursów giełdowych
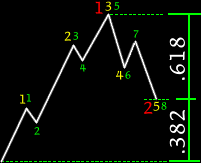
W Teorii Fal Elliotta, wszystkie główne wahania na rynkach giełdowych
są opisane przez serie pięciu fal. Klasyczna seria Fal Elliotta składa
się z początkowego wahnięcia ku górze, drugiego wahnięcia w dół (często
stanowiącego 61.8 % początkowego ruchu ku górze), wtedy trzecia fala (zwykle
największa) stanowi wahnięcie znowu ku górze; potem występuje kolejny
ruch i w końcu piąta fala, która wyczerpuje serię. Ponadto, każda z głównych
fal (1, 3 i 5) może zostać rozdzielona na pod-fale itd. i zawiera inne
stosunki Fibonacciego.
[In Elliott Wave Theory, all major market moves are described by a five-wave series. The classic Elliott Wave series consists of an initial wave up, a second wave down (often retracing 61.8% of the initial move up), then the third wave (usually the largest) up again, then another retracement, and finally the fifth wave, which would exhaust the movement. In addition, each of the major waves (1, 3, and 5) could themselves be separated into subwaves, and so on, and exhibit other Fibonacci relationships.]



a. Galaktyki
b. Huragany
c. Pajęcze sieci
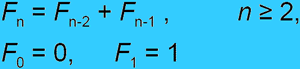




a. Kalafior
b. Eksplozja
c. Cumulus
d. Lawina

a. W falach pustynnego piasku, w tzw. szczelinach z wysychania w Dolinie Śmierci, w spękaniach geologicznych, w tzw. heksakoralach, oraz w rozbitej szybie (doświadczenie przeprowadzone przez autora) występują najczęściej pięciokąty, których budowa oparta jest na złotej liczbie. Wydaje się, że częstość występowania tam pięciokątów jak i innych wielokątów podpada pod pewną stałą regułę.
b. Pięciokąty przeważają we wszystkich skalach. W tzw. mikrocząsteczkach, w kształcie ziaren żwiru, w kształtach skorup rozbitych naczyń ceramicznych, jak również w geometrii wielkoskalowej struktury rozmieszczenia Ciemnej Zimnej Materii we Wszechświecie oraz w geometrycznej konstrukcji Wszechświata.
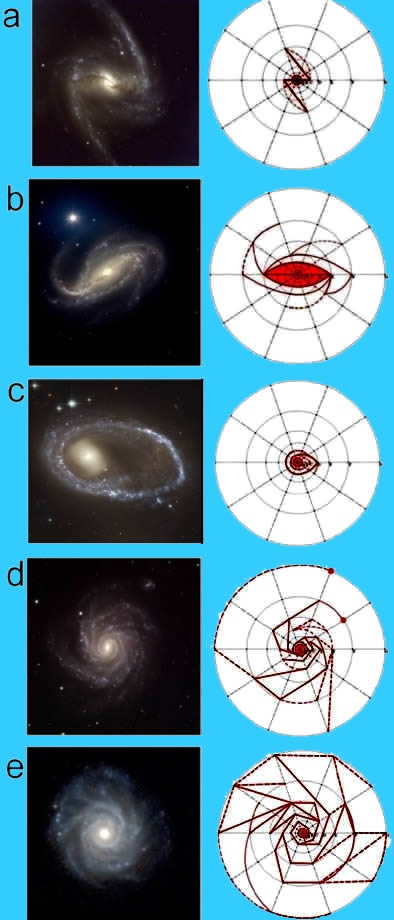
c. Złota spirala/spirala Fibonacciego w torze aksjonu w komorze pęcherzykowej, w muszli ślimaka, wirze cyklonu, w spiralnej galaktyce oraz w strukturze wielkoskalowego rozkładu galaktyk.
Geometryczne podobieństwo poszczególnych struktur zarówno w a., b., jak i w c. wydaje się niewątpliwe, jednak związek pomiędzy poszczególnymi obiektami wygląda na czysto przypadkowy.

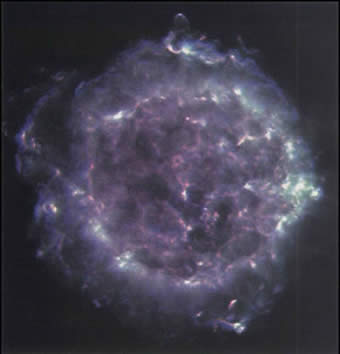

„Piaskowy dolar” - Echinoderm z rodziny Clypeasteroida (klasa Echinoidea) [u góry, za: Spoke 5 - Heh - The Blessing of Life.htm].
Fale dźwiękowe układają losowo rozmieszczone cząstki we wzór geometryczny [u dołu, R. Lawlor]. Widać, że figura w środku „głównego koła” jest „łukowym pięciobokiem”.


Obecność pięciokątów w zewnętrznym pokryciu pancerników (powyżej).

Diagram wielkoskalowego rozmieszczenia materii, tzw. Las Alpha Lymana (powyżej) - tu również widoczne są pięciokąty.
[za: Wandering Through the Lyman Alpha Forest, http://zeus.ncsa.uiuc.edu:8080/LyA/minivoid.html#pubs]
„[...]
uniwersalność łamania symetrii wyjaśnia dlaczego układy żywe i nieożywione
mają tak wiele wspólnych wzorów. Samo życie jest procesem tworzenia symetrii
- reprodukcji”
„[...] taka sama podstawowa metoda tworzenia wzorów, ten sam mechanizm
łamania symetrii we wszechświecie wytworzonym masowo rządzi kosmosem,
atomem i nami”
„[...] pradawny przypadek przenoszony przez masową technikę replikacji”
I. Stewart, op. cit., s. 109.
Przypadek panuje we wszystkich dziedzinach dostępnych dzisiaj naszemu poznaniu, poczynając od świata cząstek elementarnych, z którego w sposób mniej lub bardziej „przypadkowy” powstają atomy. W świecie procesów atomowych i molekularnych gra przypadku jest szczególnie wyrazista: nie są z niej też wyłączone ani aminokwasy, ani proteiny, które [...] nazwaliśmy „gotowymi elementami życia”. Procesy przypadkowe odgrywają taką samą rolę w martwej materii nieorganicznej, jak i w żywych substancjach organicznych. W materii żywej są one po prostu łatwiejsze do zauważenia.
Fuchs, W.R., Pod obcymi słońcami, Warszawa 1976.
Ludwig
Wittgenstein
(1889-1951)

Wszystko, co się dzieje i zachodzi, jest przypadkowe. Co zaś czyni je nie-przypadkowym, nie może być w świecie, bo wtedy byłoby znowu przypadkowe. Musi leżeć poza światem.
L.
Wittgenstein, Tractatus
logico-philosophicus, 6.41,
tłum. B. Wolniewicz, Warszawa 2002.
G.W. Leibniz
Jeśli to, co dane, jest uporządkowane, to także to, co nieznane, kryjące się poza zjawiskami, jest dziedziną ukrytego porządku. Porządek wskazuje porządek. Ponieważ w świecie bezpośrednio nas otaczającym przeważa porządek, więc w istocie wszystko jest dziedziną porządku. Nawet poza chaosem kryje się porządek.
J. Perzanowski, op. cit., s. 268.
Albert Einstein (1879-1955)

Wierzę w Boga Spinozy,
który objawia się w harmonii istnienia.
Denis
Brian, Albert Einstein,
tłum. Jarosław Bielas i Maria Zborowska, Warszawa 1997, s. 129.
Nie istnieją absolutnie przypadkowe rozkłady elementów

Jeśli bowiem chodzi o porządek powszechny, wszystko jest z nim zgodne. A to jest tak prawdziwe, że nie tylko nie dzieje się w świecie nic, co by było bezwzględnie nieprawidłowe, ale nawet niepodobna nic takiego na pozór wywołać. Dla przykładu załóżmy, że ktoś postawił na chybił trafił kilka punktów na papierze, jak to robią ci, którzy uprawiają śmieszną sztukę geomancji; twierdzę, że można znaleźć linię geometryczną, której pojęcie zgodnie z pewnym prawidłem byłoby stałe i jednolite, tak że linia ta przechodziłaby przez wszystkie te punkty, i to w takiej kolejności, w jakiej stawiała je ręka. Jeśli zaś ktoś nakreślił jednym ciągiem linię, która byłaby raz prosta, raz kolista, raz znowu innej natury, to można znaleźć pojęcie lub prawidło, lub też równanie wspólne dla wszystkich punktów tej linii, na mocy którego te same zmiany muszą nastąpić. I nie istnieje na przykład twarz, której kontur nie tworzyłby odcinka linii geometrycznej i przy pewnym prawidłowym ruchu nie mógłby być nakreślony jednym pociągnięciem. Wszelako gdy dane prawidło jest bardzo złożone, zgodnie ze swymi właściwościami, od razu uchodzi za nieprawidłowe. Można zatem rzec, że jakkolwiek Bóg byłby stworzył świat, zawsze byłby on prawidłowy i objęty pewnym ogólnym porządkiem. Wszelako Bóg wybrał ten, który jest najdoskonalszy, tzn. ten, który jest równocześnie najprostszy w swych założeniach, a najbogatszy w skutkach, czym by mogła być linia geometryczna, której budowa byłaby łatwa, własności zaś i zastosowania godne podziwu i bardzo rozległe.
G.W. Leibniz, Rozprawa metafizyczna, tłum. S.
Cichowicz,
w: G.W. Leibniz, Wyznanie wiary filozofa, PWN 1969, s. 102-103.
Rys. Niemożliwe jest pomyślenie, wyobrażenie sobie, ani narysowanie absolutnie chaotycznego rozkładu elementów - a. Ten rozkład jest zbyt równomierny na to, aby był chaotyczny - b. Ten jest zbyt „skupiony” - c. Ten rozkład punktów wydaje się jchaotyczny, ale (d) istnieje funkcja (relacja, reguła), łącząca te wszystkie punkty ze sobą i pokazująca, że w ich wzajemnym ułożeniu istnieje jednak pewien subtelny porządek.

Teoria
ta zostaje wprowadzona jako logicznie konieczna.
Podejmuje ona m.in. wyjaśnienie szeregu zastanawiających zjawisk. Np.
jeśli będziemy przez odpowiednio długi czas sypać ziarna soli na stół
tak, aby miejsce upadku każdego z ziaren było zupełnie przypadkowe, wówczas
otrzymamy w końcu rozkład linii ziaren soli o wyraźnym pięciokątnym wzorze.
Jest to jedynie opis pewnego doswiadczenia myślowego, ktorego nie da sie wykonać w praktyce. W fizyce wolno stosowaę (i często stosuje się) proces idealizacji, w ktorym abstrahujemy od pewnych rzeczywistych uwarunkowań. Tak jest i w tym wypadku. W praktyce bowiem nie mamy sposobu na to, by sypać ziarna soli w sposob doskonale przypadkowy. Każde działanie ludzkie jest bowiem regularne, nawet gdy staramy się nadać mu cechy chaotyczności. Nie da się również tego procesu sypania ziaren zautomatyzować tak, by byl on procesem czysto losowym, bowiem procesy automatyczne też takie nigdy nie są. Żeby były takowymi, musielibyśmy dysponować jakimś generatorem liczb losowych. Zaś - jak pokazal to już twórca techniki komputerowej John von Neumann - wszelkie nasze takie generatory są tylko generatorami liczb pseudolosowych.
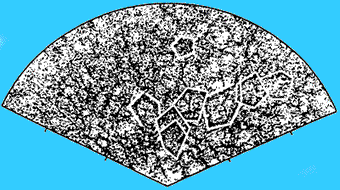
Reguła przypadku – miara µ prawdopodobieństwa spontanicznego wystąpienia proporcji g:
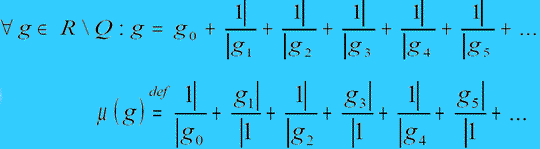
Dla liczb wymiernych:
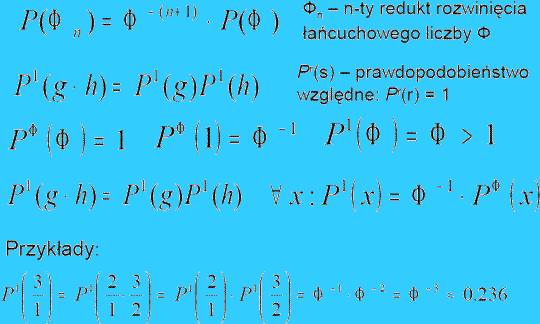
Wenus
zwraca stale te samą swoja stronę ku Ziemi, czego nie tłumaczy teoria
grawitacji.
Jest to jednak spowodowane przypadkową zbieżnością stosunków: orbitalnych
okresów Wenus i Ziemi (8/13) oraz okresu obrotu Wenus do okresu orbitalnego
Ziemi (2/3). Są to stosunki sąsiednich liczb Fibonacciego, których prawdopodobieństwo
przypadkowego wystąpienia jest wysokie.
Co prawda szansa zbiegnięcia się tych stosunków w pojedynczym przypadku
jest niska, ale ponieważ istnieje w Układzie Słonecznym 8 par sąsiednich
planet, zatem szansa że wystąpi coś takiego w którejś z tych par jest
już znacznie większa.
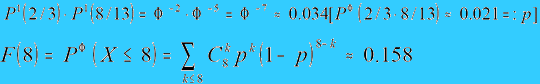
Przybliżony wykres miary (względnego) prawdopodobieństwa na liczbach rzeczywistych
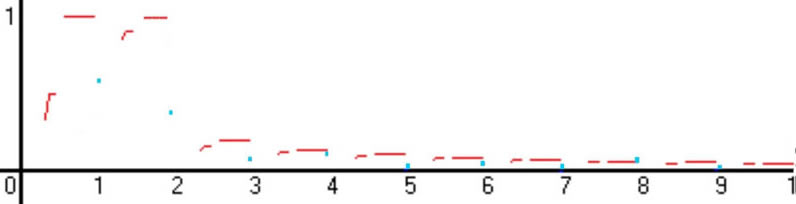
Teoretyczne prawdopodobieństwo przypadkowego wystąpienia niektórych proporcji:

liczba g __rozwinięcie
łańcuchowe liczby g
Teoretyczny
rozkład prawdopodobieństwa przypadkowego występowania wielokątów foremnych
w naturze (górny panel): dla każdego wielokąta iloczyn prawdopodobieństw
wystąpienia stosunku sąsiednich przekątnych, wzgl. małej przekątnej i
boku.
Panel dolny: przypadkowe kształty odłamków naczyń ze stanowisk archeologicznych
mogą być przybliżane przez odnośne foremne wielokąty.
Zawisza K., A New Probabilistic Measure... op. cit.
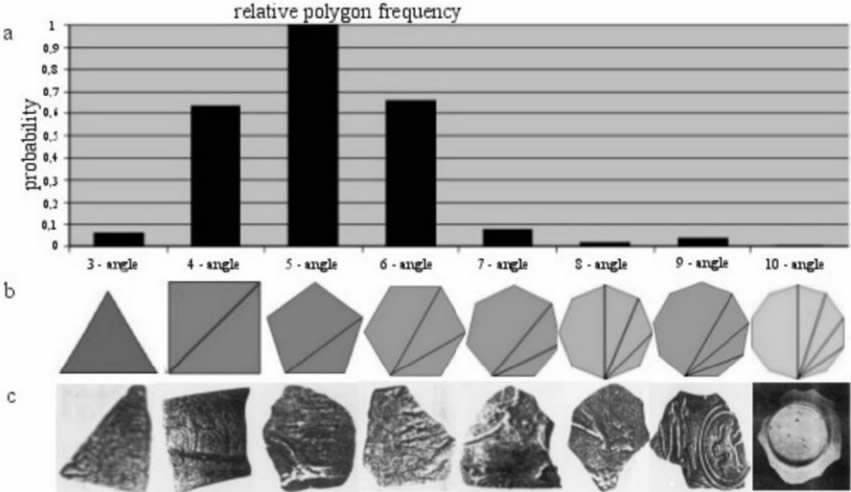
relative polygon frequency - względna czętostość występowania danych wielokątów
probability - prawdopodobieństwo
n-agle - n-kąt
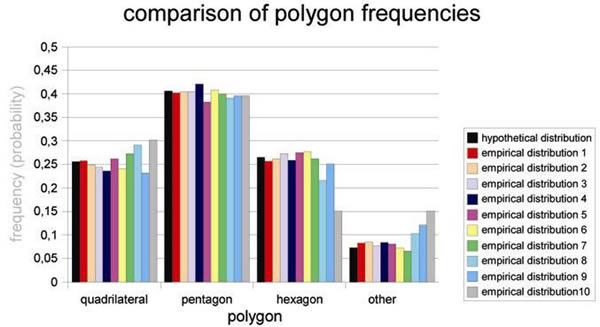
comparison of polygon frequencies - porównanie częstości występowania wielokątów
frequency (probability) - częstość (prawdopodobieństwo)
hypothetical distribution - rozkład hipotetyczny
empirical distibution - rozkład empiryczny
polygon - wielokąt
quadrilateral - kwadrat
pentagon - pięciokąt
hexagon - sześciokąt
other - inne

Szansa znalezienia asteroidy na orbicie o hamiltonianie Hp
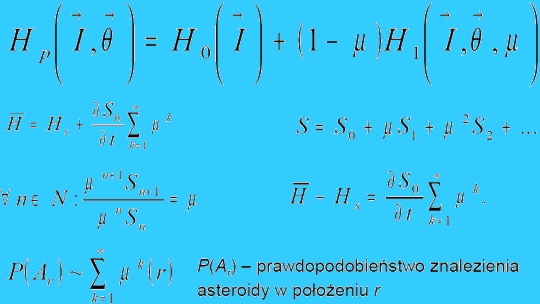

main belt asteroids - asteroidy Pasa Głównego
kuiper belt asteroids - asteroidy Pasa Kuipera
Number of know asteroids - liczba znanych asteroidów
Distance from Sun - odległość od Słońca
Orbital period - okres obrotu
Jupiter's orbital period - okres obrotu Jowisza
probability - prawdopodobieństwo
resonance - rezonans
theoretical - teoretyczny
empirical - empiryczny
 gdzie
n = 1, 2, 3, …
gdzie
n = 1, 2, 3, …Wykres ulega wyraźnemu „wyostrzeniu”

...
co jest zgodne z twierdzeniem Downarowicza-Lacroix

a - przyciąganie , b - niezależność , c - odpychanie
Astronomia
Teoria Względności
Teoria strun
Splątanie kwantowe
Teoria ewolucji
Teoria gier hazardowych
Teoria rynków giełdowych
Światopogląd naukowy
Teologia
I zapewne wiele innych
Najbardziej
prawdopodobne warunki brzegowe cyklonów i galaktyk spiralnych: a’b’/b’c’
= b’c’/c’d’ = c’d’/d’e’ = d’e’/e’f’ = a’’b’’/b’’c’’ = b’’c’’/c’’d’’ =
c’’d’’/d’’e’’ = d’’e’’/e’’f’’ ![]() 0A/AB = AB/BC = BC/CD = CD/DE = DE/EF = EF/FG =
0A/AB = AB/BC = BC/CD = CD/DE = DE/EF = EF/FG = ![]() .
.


Wybrane
wartości funkcji gęstości prawdopodobieństwa odległości od Słońca spodziewanej
11-stej planety

Dx - średnia odległość
od Słońca 10-tej planety Eris = 64.236 AU
Relative
distance - odległość względna
Absolute distance - odległośc absolutna
semi-major axis - wielka półoś orbity
Relative probability of finding 11th planet - względne prawdopodobieństwo
znalezienia 11-tej planety
K. Zawisza, op. cit.
[Imposing
probabilistic interpretation upon functions such as the Lorentz transform
![]() ,
running through the probability scope of [1, 0], whereas
,
running through the probability scope of [1, 0], whereas ![]() runs
through an analogous scope [0, 1]. Higher speed of a body means, in this
case, higher probability of occurrence of the same within a given space-time
area. (Similarly, the faster the move of a pendulum, the higher the chance
of its being met in a given time and within a given section of its trajectory).
Putting the Lorentz transform as
runs
through an analogous scope [0, 1]. Higher speed of a body means, in this
case, higher probability of occurrence of the same within a given space-time
area. (Similarly, the faster the move of a pendulum, the higher the chance
of its being met in a given time and within a given section of its trajectory).
Putting the Lorentz transform as ![]() and
interpreting, in general, a module being higher than one in terms of ‘absolute
probability’ (i.e. probability that an event may occur in case there are
more reasons therefore than as sufficient for occurrence thereof), we
should be hoping for gaining a more in-depth insight in the nature of
certain phenomena and processes.]
and
interpreting, in general, a module being higher than one in terms of ‘absolute
probability’ (i.e. probability that an event may occur in case there are
more reasons therefore than as sufficient for occurrence thereof), we
should be hoping for gaining a more in-depth insight in the nature of
certain phenomena and processes.]
Leżącą
u podstaw teorii strun funkcję beta Eulera [Euler beta function]
![]() ,
można zinterpretować
probabilistycznie (tym bardziej że występuje już ona w funkcji beta gęstości
prawdopodobieństwa) i zgodnie z Regułą Przypadku, utożsamiając m
z µ. Także w teorii superstrun częstość drgania struny można utożsamić
z częstością występowania opisywanej równaniem struny cząstki lub zjawiska.
Z kolei macierze w macierzowej teorii superstrun, gdzie występujące już
macierze losowe, można rozpatrywać jako macierze procesów Markowa.
,
można zinterpretować
probabilistycznie (tym bardziej że występuje już ona w funkcji beta gęstości
prawdopodobieństwa) i zgodnie z Regułą Przypadku, utożsamiając m
z µ. Także w teorii superstrun częstość drgania struny można utożsamić
z częstością występowania opisywanej równaniem struny cząstki lub zjawiska.
Z kolei macierze w macierzowej teorii superstrun, gdzie występujące już
macierze losowe, można rozpatrywać jako macierze procesów Markowa.
Ibid.
[The
Euler beta function: ![]() , being
the underlying concept for the theory of strings, may be interpreted in
probabilistic terms (all the more that it already appears in the probability
beta density function) as well as in accordance with the rule of chance,
whereby m is identified with µ. Also, in the theory of superstrings,
the string vibration frequency may be identified with the frequency of
occurrence of the particle or phenomenon described using the string formula.
In turn, matrices in the matrix superstring theory where random matrices
already appear, can be considered as Markov process matrices.]
, being
the underlying concept for the theory of strings, may be interpreted in
probabilistic terms (all the more that it already appears in the probability
beta density function) as well as in accordance with the rule of chance,
whereby m is identified with µ. Also, in the theory of superstrings,
the string vibration frequency may be identified with the frequency of
occurrence of the particle or phenomenon described using the string formula.
In turn, matrices in the matrix superstring theory where random matrices
already appear, can be considered as Markov process matrices.]
W
klasycznej teorii informacji z rozkładem prawdopodobieństwa ![]() można
związać entropię Shannona:
można
związać entropię Shannona: ![]()
Jeżeli system nadrzędny znajduje sie w czystym stanie kwantowym, entropia
jednego podsystemu może zostać użyta, by zmierzyć jego stopień związku
z innymi podsystemami.
![]()

Drzewo filogenetyczne
i i drzewo Fibonacciego
„Drzewo” mutacji i selekcji
Teoria gier hazardowych [1]

Po serii określonych
wyników, należy zawsze stawiać na inne.
Z kolei grając w totka zwiększamy szansę wygranej, jeśli kolejne różnice
pomiędzy skreślonymi liczbami będą kolejnymi liczbami Fibonacciego. Np.:
44, 42, 39, 34, 26, 13; 8, 10, 13, 18, 26, 39 itd.
Jak pisze znany francuski matematyk Emil Borel odnośnie serii tych samych wyników rzutu monetą: „Należy [...] uznać za znikome nadzieje matematyczne, które by liczyły ponad 25 rzutów; partie takie, praktycznie rzecz biorąc, nigdy się nie zdarzają.”
E. Borel, Prawdopodobieństwo i pewność, tłum.
A. Zabłudowski, W-wa 1963, s. 129.
Zatem, jeśli doczekamy się (w jakiejś grze) serii 25 kolejnych orłów (resp. reszek), mamy praktyczną pewność, że stawiając teraz na reszkę (resp. orła) – wygramy.
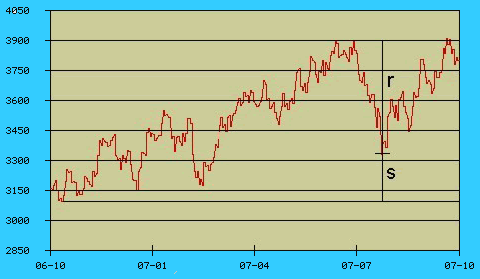 P(r/s)~µ(r/s)
P(r/s)~µ(r/s)Korzystając z teorii przypadku możemy także prognozować prawdopodobieństwo określonych stosunków czasowych pomiędzy kolejnymi hossami (bessami).

Stosunek długości okresów pomiędzy kolejnymi hossami (bessami) dąży z największym prawdopodobieństwem do stosunku kolejnych liczb Fibonacciego.


Skoro nawet przypadek podlega stałym regułom kurczy się miejsce na nadnaturalną interwencję. Wszystko, co jest, jest na zasadzie logicznej konieczności. Zostaje jednak kwestia tożsamości: musisz istnieć ty i ja, ale dlaczego to ja jestem mną, a ty – tobą, a nie odwrotnie?
Wniosek
Końcowy
Wszechświat
jest kosmosem
[grec. kosmos – przypadek lub ład.]