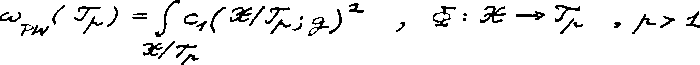|
E. Kählerowi
Stanisławowi Michalskiemu
i Zygmuntowi Janiszewskiemu
W niniejszym artykule
zastanawiam się nad istotą matematyki i opisuję dziwnie późne,
bo dopiero w XIX wieku, pojawienie się szkół matematycznych (a przecież
szkoły filozoficzne istniały już w klasycznej starożytności!). Próbuję
uprzytomnić i uzmysłowić to cudowne
zjawisko, jakim były narodziny Polskiej Szkoły Matematycznej (PSM) i jej
życie we Lwowie i Warszawie. Nasza epoka straciła zmysł cudu, organ
percypowania cudu jest w atrofii. Powiada się: „cudów nie ma - bo ich
być nie może”, panuje lęk przed cudownością. Powstały całe
filozofie i nauki starające się eliminować wydarzenia cudowne:
historycyzm, socjologizm, psychologizm, ekonomizm. Cud - to pojawienie się
i życie czegoś zupełnie nowego, nieoczekiwanego - i czymś takim było
pojawienie się PSM.
Jedną z mych tez jest, że ów cud był przejawem większego
cudownego procesu, jakim był renesans narodu, obudzenie się jego sił twórczych,
zrozumienie i wiara w naukę (i sztukę) pielęgnowaną tu i teraz.
Przejawem tego był niezwykły pęd do samouctwa, a owocem - niespotykane
dotąd w świecie, bezprecedensowe wydawnictwo: Poradnik
dla Samouków, dziecko Stanisława
Michalskiego (I wyd. 1907, II - 1913/14). Najciekawszym jego tomem była Matematyka,
redagowana i w dużej mierze napisana przez młodziutkiego, genialnego
Zygmunta Janiszewskiego - ojca PSM. Nieprzypadkowa to koincydencja.
Zapewne prace nad Poradnikiem nasunęły Janiszewskiemu ideę
nowego nurtu w matematyce, nazwanego później - PSM. Ale PSM to nie tylko
grupka młodych, genialnych ludzi, to także nowy styl życia i
„pracy” matematycznej: atmosfera i aromat beztroskiej twórczej zabawy
- radość tworzenia bez myśli o karierze naukowej i publikowaniu.
Siedzibą i centralą owego życia była kawiarnia Szkocka
we Lwowie.
Legenda PSM musiała powstać. Legenda to nie tylko baśniowy opis
dokonań dawnych bohaterów - czy będą to mnisi buddyjscy, czy apostołowie
i święci wschodniego Kościoła - to nie kronika życia mistyków
suffijskich, czy cadyków chasydzkich, przygód „rycerzy okrągłego stołu”
króla Artusa - poszukiwaczy świętego Graala. W legendzie żyje wielki
impuls, który powodował owych bohaterów do czynów niezwykłych, ważnych
dla całej ludzkości. Dlatego legenda chce być opowiadana i czytana.
Zapomnienie o owych dokonaniach i cierpieniach to bardzo poważna choroba
- amnezja.
Ulegają jej nie tylko poszczególni ludzie, lecz całe narody. Praca
niniejsza jest także próbą przeciwdziałania owej amnezji.
Czym jest
matematyka?
Istnieje szereg bardzo poważnych trudności ujęcia istoty matematyki
(m.), a oto najpoważniejsze z nich:
1. M. współczesna jest niemal niedostępna dla nie-matematyka i to głównie
z powodu niesłychanego bogactwa pojęć - są ich tysiące! Nawet
specjaliście jakiegoś działu m. trudno porozumieć się z kolegą
pracującym w innym dziale. M. była i jest wiedzą ezoteryczną.
2. Panuje - nie tylko wśród „profanów” - zupełnie fałszywe wyobrażenie
o m., np. że komputery usuną potrzebę uczenia się jej.
3. Powyższe punkty pokazują dobitnie, że jest niemal niemożliwe - w krótkim
artykule, przeznaczonym przecież dla szerszego kręgu odbiorców - dać
wyobrażenie o naturze szkoły matematycznej.
4. W szerokich kręgach naszego społeczeństwa panuje „legenda PSM”,
która, niestety zupełnie odbiega od istoty i historii PSM.
Mimo powyższych trudności, obiekcji i niebezpieczeństwa „szargania świętości”
podaję następującą charakterystykę: M. jest: a) językiem i b)
pismem, c) sztuką,
d) życiem idei
i, oczywiście, e) nauką f) logosem fizyki.
M. jest bardzo bogatym językiem w pojęciu, jakie wypracowała współczesna
hermeneutyka, zbliżonym do prastarej, symboliczno-mistycznej teorii języka.
Dopiero język tworzy rzeczywistość, bez języka nie ma rzeczywistości.
Na pytanie: kto mówi językiem, Heidegger odpowiada: „mowa (język) mówi”.
Innymi słowy Logos (mowa) kształtuje rzeczywistość, przez człowieka mówi
Logos. Mało tego: Logos jest potęgą, która jednak potrzebuje „współpracowników”
w nieprzerwanym tworzeniu rzeczywistości (creatio
continua). Świat idei nie jest
gotowy, jest raczej nie uformowaną potężną energią, zespołem kiełków
idei ( logoi spermatikoi
- logosy nasienne), które do swego pełnego ukształtowania
potrzebują ludzkości. Jeszcze inaczej: owe kiełki idei „chcą” być
poznawane i kształtowane, „chcą” się rozwijać, „poszukują”
gleby i szansy rozwoju. Jest nią ludzkość, przede wszystkim potencjalni
twórcy: poeci, artyści, filozofowie, uczeni. W przypadku dziwnego
logosu, jakim jest m. - potrzebują i poszukują ludzi zwanych
matematykami. Ale, podobnie jak inne języki (np. j. polski, czy muzyka),
do przekazywania twórczej energii konieczni są także „zwyczajni
ludzie” (rodzice przekazujący dziecku mowę ojczystą, nauczyciele
muzyki, matematyki). Przecież nawet największy matematyk potrzebował
nauczyciela „szkolnej matematyki”.
Ale nie każdy język dysponuje pismem! M. nie da się pomyśleć bez
niezwykle bogatego pisma, nie ma m. bez tysięcy znaków ( często zwanych
„symbolami matematycznymi” ). Jak podkreślał Kähler - matematyka
jest pismem.
Skoro m. jest życiem idei - rozwijających się, zapładniających
nawzajem, umierających, rodzących się na nowo w nowej postaci - to
zrozumiałe staje się jej wielkie znaczenie dla filozofii. Platonicy
zdawali sobie zawsze sprawę, że najlepszym - o ile nie jedynym - dostępem
do świata idei (kosmos,
noetos), propedeutyką filozofii jest matematyka. Legendarny napis
przy wejściu do „akademii platońskiej” głosił: „- Niech nie
wkracza tu nikt, kto nie zna geometrii (matematyki)”. Może teraz nie
wyda się zaskakująca piękna wypowiedź Kählera (z r. 1939):
M. jest organem poznania i niesłychanym
usubtelnieniem języka potocznego. Wznosi się z języka potocznego i świata
wyobrażeń jak roślina z gleby, a jej korzeniami, są liczby i proste
wyobrażenia przestrzenne. Nie wiemy jeszcze jaka to treść domaga się języka
matematyki. Nie możemy nawet przeczuwać, w jakie dole i głębie pozwoli
spojrzeć ludziom to duchowe oko, jakim jest matematyka.
Udział człowieka w życiu idei
nazywa się poznawaniem.
Największy ma tematyk XX stulecia, Hermann Weyl, podkreślał zawsze
jedność matematyki. i fizyki (był on także wybitnym fizykiem i
interesującym filozofem!). Jedność ta, dla dawnych pokoleń była tak
oczywista, że fizyków do niedawna jeszcze nazywano „geometrami” lub
„matematykami”. Dla wielu matematyków, a także fizyków wieku (w
tym, niestety, dla PSM), jedność ta przestała być oczywista. Stąd częste
zdziwienie i zachwyt dla „niezrozumiałej adekwatności matematyki i
fizyki” (E. Wigner). Ostatnia znów wybitni matematycy i fizycy są świadomi
jeśli nie jedności, to zapładniającej roli owych „dwóch różnych
nauk”. Interesująca jest w tym względzie ewolucja spojrzenia wielkiego
Einsteina na matematyk. Młody Einstein miał do matematyki stosunek niechętny
(słabo ją znał), później zaś uważał (fałszywie!), że „w fizyce
naprawdę twórczym elementem jest matematyka”.
Czym jest Szkoła matematyczna?
Zasadniczą cechą wszelkiej
szkoły jest relacja nauczyciel - uczeń, czy też mistrz - uczeń.
Nie wszystkim było dane mieć prawdziwego nauczyciela mistrza). Trzeba
sobie uprzytomnić, że każdy człowiek ma dwojakiego
rodzaju rodziców i przodków: biologicznych
oraz duchowych - właśnie nauczycieli. Ta druga, „pionowa” (w odróżnieniu
od pierwszej „poziomej”) relacja nazywa się filiacją. To, co
powiedziane było o życiu idei i roli ludzi w owym procesie czyni pojęcie
filiacji niemal oczywistym. W życiu idei matematycznych musimy rozszerzyć
pojęcie nauczyciela - mistrza, duchowego ojca” także na ludzi nie
spotkanych bezpośrednio. Dla wielu matematyków dużo ważniejsze były
publikacje nieżyjących już
badaczy (interesująca jest
analogia z podstawową ideą ezoteryki żydowskiej „Szkoły - objawienia
Proroka Eliasza”), niż ich kontakt z żyjącymi, nie zapładniającymi
ich duchowo nauczycielami uniwersyteckimi. Tradycja matematyczna jest
zatem filiacją. A więc dla twórczości matematycznej nie jest konieczna
„szkoła matematyczna”, która - jak wspomnieliśmy - jest rzadkim
zjawiskiem w życiu m., trwającym ponad 2590 lat.
Każda ze szkół ma swych ojców, ma swą tematykę badań, styl pracy.
Na czym polegał cud powstania, specyficzność PSM? Wielkie, płodne
idee, ważne inspiracje potrzebują przygotowanego gruntu, są to właśnie
kiełki, nasiona, które chcą wzejść w umysłach i sercach ludzi. Często
rolę ich pełnią outsiderzy, nie należący da żadnego
„establishmentu”, a więc nie wyżsi urzędnicy ani też członkowie
hierarchii wyższych uczelni. Mocne, sztywne struktury akademickie -
aczkolwiek pożyteczne, a nawet konieczne - bardzo silnie kształtują
swych członków i często patrzą podejrzliwie na zupełnie nowe
koncepcje, czy idee. Przykładów jest legion: kościoły i sekty,
medycyna uniwersytecka patrząca niechętnie na „ medycyny
alternatywne” (np. homeopatię, akupunkturę), historia psychoanalizy.
czy jungowskiej psychologii głębi, przemysł farmaceutyczny bojkotujący
różnego rodzaju preparaty ziołowe, homeopatyczne itp. Tak zapewne było
zawsze, tak jest i „być musi”. Nowe jest zupełnie obce i niedoskonałe,
pozornie słabe, ale żyje w nim niezwykła duchowa siła. Wczesne chrześcijaństwo
zwalczane było przez ówczesny establishment - synagogę. Gdy okrzepło i
stało się potężną instytucją, zwalczało bezwzględnie wszelkie nowe
ruchy, nazywając je herezjami. Młody chasydyzm zwalczany był zajadle
przez rabinat, który nie cofał się nawet przed fałszywymi donosami do
władz carskich.
Życie i działalność Stanisława Michalskiego
jest przejmującą ilustracją powyższych
ogólnych rozważań. Młody inżynier, absolwent politechniki
moskiewskiej, Wołyniak - organizuje jeszcze w Moskwie bibliotekę Związku
Młodzieży Akademickiej. Biblioteka mieściła się w sali rysunkowej
Politechniki, a „bibliotekarz miał dużo kłopotu z doborem książek i
lektury dla kolegów”. Jeszcze
bardziej odczuwał potrzebę wskazówek, gdy przybył w roku 1890 do
Warszawy, gdzie jako mody inżynier pracował w fabryce Rudzkiego. Później,
gdy przeniósł się na „Kolej Wiedeńską”, zaczął sprawować
nieoficjalną funkcję „kolejowego ministra oświecenia publicznego”.
Jeszcze wcześniej zajął się legalną pracą oświatową, którą właściwie
rozwinął i pozostawił na należytym poziomie. Był duszą i, przez
dziesiątki lat, sekretarzem Towarzystwa Dobroczynności w Warszawie -
instytucji założonej przez J.T. Lubomirskiego w roku 1861. „Wszystkie
prace, do których wchodził młody inżynier, nabierały mocy i barwy i
stawały się ważnymi placówkami kulturalnymi. Michalski umiał w nie
wlać energię, wolę wytrwałą pracę” (podkr. K. M.).
Czytelnie stały się szybko ośrodkiem pracy dziesiątków i setek ludzi
dobrej woli, którzy niezależnie od przekonań, prowadzili wspólną
pracy oświatową.
Trzeba uprzytomnić sobie atmosferę tamtych czasów w Kongresówce.
Warszawa i całe Królestwo żyło niezwykle intensywnym życiem
podziemnym. Świetne ujęcie problemów i atmosferę tamtych czasów
zawdzięczamy klasycznej dziś już monografii Bogdana Cywińskiego Rodowody
Niepokornych. (Pamiętam, jak na
kilka lat przed napisaniem owej słynnej książki, przyszedł do mnie jej
Autor, proponując mi współpracę nad nią. Musiałem mu wtedy odmówić
- nie byłem kompetentny, a nadto zajęty pisaniem monografii i podręczników
matematycznych, pracą nad budową nowej katedry. Częściowo spłacam ów
„dług” niniejszym artykułem.) Wystarczy wspomnieć w tym miejscu
„Latający Uniwersytet” (dokładniej: „Kursy Lotne Naukowe”). Te
tajne wykłady na poziomie uniwersyteckim były osobliwością Królestwa
i trwały do roku 1905. (Idea odżyła w czasie okupacji hitlerowskiej,
nigdy młodzież nasza nie uczyła się z takim zapałem i oddaniem, z dosłownym
narażeniem życia. Dane mi było - jako studentowi - brać udział w tym
niezwykłym wydarzeniu!)
Pamiętajmy, był to okres polskiego „pozytywizmu”, „organicznej
pracy od podstaw”, samouctwa. Zdawano sobie jasno sprawę, że „nauka
to potęga”, że nie będzie Polski bez polskiej kultury i nauki.
Ofiarność i bezinteresowność owej epoki jest niemal nie do pojęcia
dziś, gdy panoszy się malkontenctwo, jałowa zawiść i „prywata”.
Na tamten grunt padały nasiana rzucane i pielęgnowane przez Michalskiego
i jego współpracowników. Kiełkowała w nim idea Poradnika
dla Samouków, pracowała w jego
podświadomości i długo go męczyła. „Michalski od najwcześniejszej
młodości miał aspiracje naukowe, jakąś romantyczną tęsknotę do
nauki. Zajmował się w szkole wyższej gruntownie matematyką, a
później tęsknił za psychologią i pedagogiką. Początki idei Poradnika
zrodziły się w 1897 r. Pomógł mu Aleksander Hefllich, prokurent
bankowy i ideowy pracownik czytelni bezpłatnych, obejmując techniczną
organizację wydawnictwa. Obaj stworzyli bezinteresowną spółkę
wydawniczą, której celem miało być wydanie Poradnika,
obliczonego na 3-4 tomy. Mimo że idea Poradnika
leżała niemal na ulicy, to jednak zrozumienie zasad przyszłego
wydawnictwa spotykało się z dużym oporem specjalistów. Poradnik
od razu stał się ośrodkiem impulsów, tętniącym nowym życiem.
Mieszkanie Michalskiego przy ulicy Nowogrodzkiej przekształciło się w
istną siedzibę naukową. Schodzili się tam wszyscy, proszeni i
nieproszeni, uczeni i dyletanci, młodzież szukająca wiedzy i pomagająca
w pracy. Wydawnictwa nabrało rozgłosu, zwłaszcza po wydaniu - z pomocą
Kasy Mianowskiego - I tomu. Książka, wydana w 2,5 tys. egzemplarzy,
rozeszła się w ciągu 1-2 miesięcy, wywołując powszechny entuzjazm i
niecierpliwe wyczekiwanie reszty tomów.
Dla nas niezwykle cenne jest porównanie pierwszego wydania Poradnika
z drugim. Pierwsze jest jeszcze bardzo skromne, stosunkowo mało ambitne,
bardzo elementarne, zwracające się do szerokiej rzeszy czytelników, mających
jedynie podstawowe przygotowanie. Wydanie drugie jest dziełem zupełnie
nowym, przede wszystkim zaś tom poświęcony matematyce. Dopiero to dzieło
zadowoliło Michalskiego w zupełności. Nie byłoby ono jednak do pomyślenia
bez niezwykłej, twórczej inicjatywy młodziutkiego Zygmunta
Janiszewskiego.
Narodziny
Polskiej Szkoły Matematycznej
Niedługo po zakończeniu II wojny światowej zaczął działać,
oficjalnie już, Uniwersytet Warszawski. Było nas około 30 studentów
sekcji matematyczne-fizycznej wydziału „matematyczno-przyrodniczego”,
bez podziału na lata studiów. Pamiętam niewiele wykładów kursowych i
monograficznych oraz dwa seminaria (w tym jedno na bardzo elementarnym
poziomie). Na wykłady z matematyki i fizyki uczęszczali wspólnie
studenci chcący poświęcić się matematyce bądź fizyce. Seminarium
Matematyczne gnieździło się w trzech maleńkich pomieszczeniach odstąpionych
gościnnie przez Instytut Fizyki Doświadczalnej. Jeden pokój zajmowała
biblioteka z księgozbiorem Samuela Dicksteina, przeniesiona z Pałacu
Staszica, drugi służył wykładom monograficznym i seminariom, trzeci był
wspólnym gabinetem naszych wybitnych nauczycieli: Sierpińskiego,
Kuratowskiego, Borsuka, później Nikliborca i Mazura.
W tym czasie dane mi było spotkać się z niezwykłym człowiekiem,
przyjacielem Janiszewskiego i Micha1skiego, wielkim badaczem lodów,
geologiem, Stanisławem Bronisławem Dobrowolskim. Człowiek ten był
ucieleśnieniem niezwykłej epoki, w której powstał m.in. Poradnik
dla Samouków i rodziła się
Polska Szkoła Matematyczna. Ów starszy już wówczas człowiek
promieniował pogodną, pozytywistyczną wiarą w naukę, która stanowiła
dla niego prawdziwą religię. Gdy Dobrowolski dowiedział się, że chcę
poświęcić się matematyce, opowiedział mi o swym spotkaniu z
Janiszewskim, kiedy był świadkiem bólów porodowych PSM. Postaram się
wiernie oddać słowa Dobrowolskiego, bo nie chciałbym, by zeszły ze mną
do grobu:
Było to na kilka lat przed wybuchem
I wojny. Lato spędzałem w zaprzyjaźnionym dworze. Było tam sporo młodych
ludzi, pogodna atmosfera. Młodzi flirtowali, chodzili na wspólne
spacery; wieczorami grali w karty, tańczyli. Pojawia się tam któregoś
dnia miody matematyk, Zygmunt Janiszewski. Byłem jedynym, które chciał
go wysłuchać, »rozmawiać z nim«. Tygodniami chodziliśmy po dworskim
parku, polach, lesie, a Janiszewski mówił do mnie. Wylewały się z
niego matematyczne pomysły, idee. Niewiele z tego rozumiałem, ale zdawałem
sobie sprawę, że muszę go słuchać, towarzyszyć mu w jego
deliberacjach, bo inaczej on oszalałby. Dziś, po przeszło
czterdziestu latach widzę, że byłem przy narodzinach Polskiej Szkoły
Matematycznej.
Opowiadanie to uprzytamnia niemal
dotykalnie działanie idei, tutaj: matematyki. Jej przemożne parcie
przypominało stan opętania wielkiego twórcy. Możemy sobie wyobrazić,
jak szczęśliwe chwile przeżywał Stanisław Michalski mówiąc
Janiszewskiemu o idei Poradnika
i widząc, że iskra zapala się wielkim płomieniem, że przyświecająca
mu idea nabiera kształtów i siły, o której nawet w najśmielszych
swych marzeniach nie śnił.
Dar bogów
Powróćmy na koniec do charakterystyki matematyki, by podkreślić jej jedność
jako organicznej całości życia idei. Matematyka jest całością
wzajemnie powiązanych i oddziałujących na siebie organów, którymi są
poszczególni matematycy, ich ugrupowania, szkoły. Tak tłumaczy się
fakt, że: 1) konstrukcja lub odkrycie matematyczne dokonane przez jednego
matematyka, czy ośrodek badawczy, niemal jednocześnie zostaje
dokonane przez innych, mimo braku zewnętrznych kontaktów; 2) gdy jakaś
teoria matematyczna dojrzeje, rozwinie się, pojawiają się nieznane dotąd
i nieoczekiwane powiązania z odległymi dotychczas działami matematyki;
3) ale jedność ta nie jest czymś gotowym i nie zagrożonym. Musi być
ustawicznie odnawiana, przekazywana, przeżywana. Na skutek swego ogromu
współczesna matematyka jest stale zagrożona rozpadem, dezintegracją,
utratą wspólnego języka. Interesujące, że pomocna w integracji jest i
dziś fizyka - jej teoretyczne-magmatyczne problemy.
Ciągłość i trwałość matematyki jest gwarantowana w dużym stopniu
tym, że matematyka jest także pismem. Jak już wspomniałem,
ezoteryczność współczesnej matematyki związana jest z setkami (tysiącami?)
znaków matematycznych, które nie wtajemniczonemu nic nie mówią, jak
hieroglify, czy nuty. Rzeczywiście, owe „symbole” przypominają
nieraz pismo obrazkowe, hieroglify, czy pismo chińskie, które,
studiowane przez długie lata, zaczynają coraz pełniej przemawiać do
badacza, pozwalają mu mówić owym językiem, zwanym matematyką, a w
szczególnych przypadkach utalentowanych matematyków rozwijać ten język
i pismo.
Zawsze, we wszystkich religiach i ich mitach wiedziano, że język i pismo
są darami bogów. Może najpiękniej przedstawia to mitologia Greków.
Sztuki, kunszty, nauka są darem Muz (stąd musiké);
poeta, matematyk, jest tylko organem Muzy: poprzez niego śpiewa ona, sławiąc
boski twór Kosmosu (jeszcze wielki Kepler wiedział, że „matematyka
<geometria> jest archetypem piękna świata”). Wielce wymowne
jest, że muzy są dziećmi Zeusa i tytanki Mnemosyne (pamięci,
przypomnienia). Przewodnikiem Muz - musagetem
- jest Apollo, one zaś są jego organami i wysłanniczkami (angeloi).
Z początku było ich trzy: Mneme (pamięć, wspomnienie), Melete (ćwiczenie
- praxis), Aoide (pieśń, śpiew). I tak matematykę tworzy człowiek
entusiasmowany
(czyli napełniony bogami), dzięki Pamięci-Wspomnieniu (Mneme),
ustawicznym ćwiczeniom - Praxis
(Melete) i śpiewaniu czyli sztuce-kunsztowi-poezji (Aoide), tj.
pracom-publikacjom, wykładom będącym pismem-literaturą, nieraz
kunsztem-sztuką, dającą wzruszenie nie tylko estetyczne. Dziś
zapomnieliśmy, że matematyka jest darem-podarkiem, wymagającym pamięci
i ustawicznego ćwiczenia-przypominania - anamnezją, tradycją, która
„nie jest konduktem pogrzebowym, lecz ciągiem zmartwychwstań -
rodzenia się w nowej
postaci”.
Na zakończenie przytaczam piękną formułę, nad którą pracowały
przez 150 lat - począwszy od Riemanna - pokolenia największych matematyków.
Nosi on mianu wzoru Wolperta.
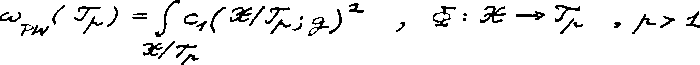
|